A Series Paper Sizes From 4A0 to A10
| Size | Width x Height (in) | Width x Height (mm) |
|---|---|---|
| 4A0 | 66.2 x 93.6 in | 1682 x 2378 mm |
| 2A0 | 46.8 x 66.2 in | 1189 x 1682 mm |
| A0 | 33.1 x 46.8 in | 841 x 1189 mm |
| A1 | 23.4 x 33.1 in | 594 x 841 mm |
| A2 | 16.5 x 23.4 in | 420 x 594 mm |
| A3 | 11.7 x 16.5 in | 297 x 420 mm |
| A4 | 8.3 x 11.7 in | 210 x 297 mm |
| A5 | 5.8 x 8.3 in | 148 x 210 mm |
| A6 | 4.1 x 5.8 in | 105 x 148 mm |
| A7 | 2.9 x 4.1 in | 74 x 105 mm |
| A8 | 2.0 x 2.9 in | 52 x 74 mm |
| A9 | 1.5 x 2.0 in | 37 x 52 mm |
| A10 | 1.0 x 1.5 in | 26 x 37 mm |
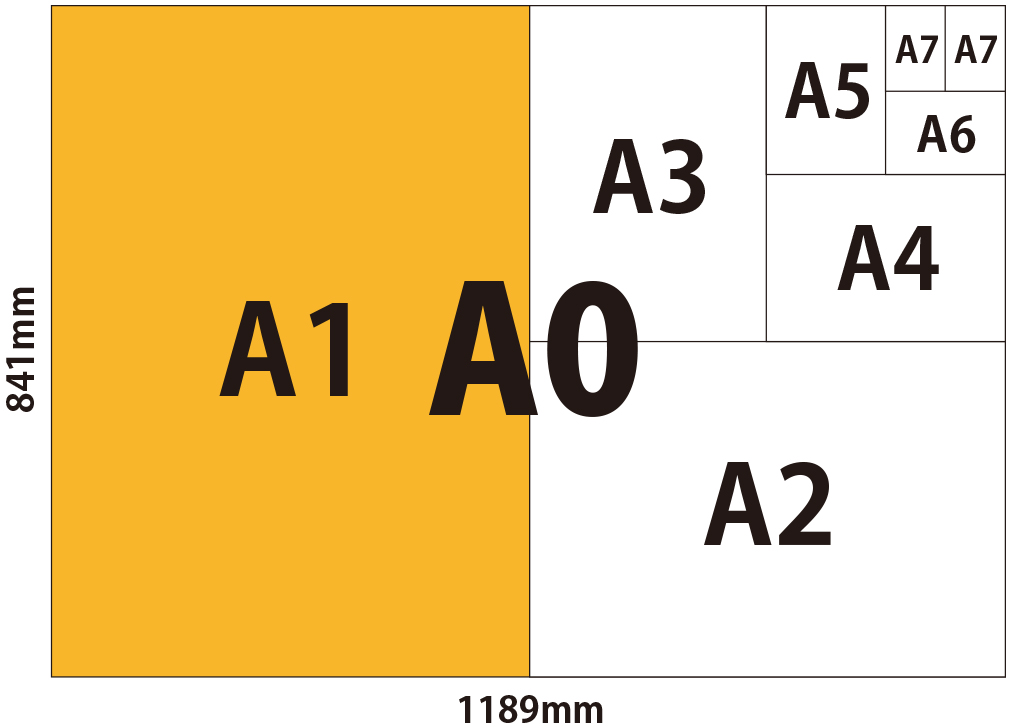
Successive paper sizes in the series A1, A2, A3, and so forth, are defined by halving the preceding paper size across the larger dimension. This also effectively halves the area of each sheet. The most frequently used paper size is A4 measuring 210 by 297 millimetres (8.27 in × 11.7 in).
The dimensions of the A series paper sizes are defined by the ISO 216 international paper size standard. The A series was adopted in Europe in the 19th century, and is currently used all around the world, apart from in the USA and Canada. The most common paper size used in English speaking countries around the world is A4, which is 210mm x 297mm (8.27 inches x 11.7 inches). The largest sheet from the A series is the A0 size of paper. It has an area of 1m2, and the dimensions are 841mm x 1189mm. The A series uses an aspect ratio of 1:√2, and other sizes in the series are defined by folding the paper in half, parallel to its smaller sides. For example, cutting an A4 in half, will create an two A5 sheets, and so forth. Any size of brochure can be made using paper from the next larger size, for example A3 sheets are folded to make A4 brochures. The standard lengths and widths of the A series are rounded to the nearest millimetre.
ISO paper sizes in portrait view (with rounded inch values)
| Format | A series | B series | C series |
|---|---|---|---|
| Size | mm × mm in × in |
mm × mm in × in |
mm × mm in × in |
| 0 | 841 × 1189 mm 33.1 × 46.8 in |
1000 × 1414 mm 39.4 × 55.7 in |
917 × 1297 mm 36.1 × 51.1 in |
| 1 | 594 × 841 mm 23.4 × 33.1 in |
707 × 1000 mm 27.8 × 39.4 in |
648 × 917 mm 25.5 × 36.1 in |
| 2 | 420 × 594 mm 16.5 × 23.4 in |
500 × 707 mm 19.7 × 27.8 in |
458 × 648 mm 18.0 × 25.5 in |
| 3 | 297 × 420 mm 11.7 × 16.5 in |
353 × 500 mm 13.9 × 19.7 in |
324 × 458 mm 12.8 × 18.0 in |
| 4 | 210 × 297 mm 8.27 × 11.7 in |
250 × 353 mm 9.84 × 13.9 in |
229 × 324 mm 9.02 × 12.8 in |
| 5 | 148 × 210 mm 5.83 × 8.27 in |
176 × 250 mm 6.93 × 9.84 in |
162 × 229 mm 6.38 × 9.02 in |
| 6 | 105 × 148 mm 4.13 × 5.83 in |
125 × 176 mm 4.92 × 6.93 in |
114 × 162 mm 4.49 × 6.38 in |
| 7 | 74 × 105 mm 2.91 × 4.13 in |
88 × 125 mm 3.46 × 4.92 in |
81 × 114 mm 3.19 × 4.49 in |
| 8 | 52 × 74 mm 2.05 × 2.91 in |
62 × 88 mm 2.44 × 3.46 in |
57 × 81 mm 2.24 × 3.19 in |
| 9 | 37 × 52 mm 1.46 × 2.05 in |
44 × 62 mm 1.73 × 2.44 in |
40 × 57 mm 1.57 × 2.24 in |
| 10 | 26 × 37 mm 1.02 × 1.46 in |
31 × 44 mm 1.22 × 1.73 in |
28 × 40 mm 1.10 × 1.57 in |
The α variables are the distinct first terms in the three geometric progressions of the same common-ratio equal to the square root of two. Each of the three geometric progressions (corresponding to the three series A, B, C) is formed by all possible paper dimensions (length and width) of the series arranged in a decreasing order. This interesting arrangement of dimensions is also very useful – not only it forms a geometric progression with easy to remember formulae, it also has that each consecutive pair of values (like a sliding window of size 2) will automatically correspond to the dimensions of a standard paper format in the series.
| A series | B series | C series | US sizes | US Envelope |
| International Envelope | Photography Paper | Canadian | Japanese | Books |
| Newspaper | Chinese | Billboard | Imperial | Colombian |
| French | Raw | Transitional |

Comments